- Worm Gear Design Calculator
- Worm Gear Design Calculation Pdf Viewer Download
- Gear Calculation Formula Pdf
- Worm Gear Design Calculation Pdf Viewer Software
DESIGN PROCEDURE FOR SPUR GEAR:
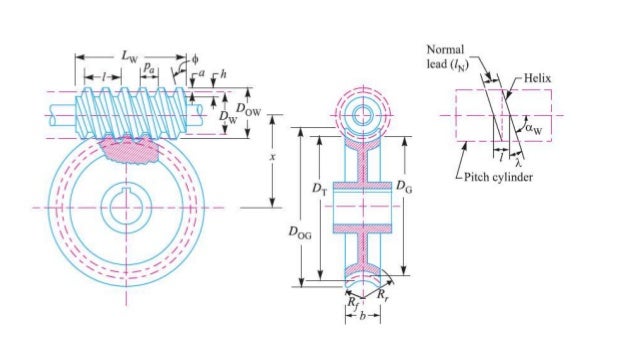
Worm Gear Design Calculation. A worm gear box must contain a worm and a mating gear (helical gear) and normally the axis of the worm is perpendicular to the axis of the gear. Look at the picture below: Where, D1 – Pitch Diameter of Worm. D2 – Pitch Diameter of Gear. C – Centre to Centre Distance between the Worm and the Gear. The individual calculations are numbered (see figure) and a list of them is shown hereinafter. By clicking on the link a full calculation listing is displayed. Specification and calculation results: vbelt01example1en.pdf. External spur gear. Specification and calculation results: Gear101example1en.pdf. PDF On Dec 31, 2014, B. Magyar and others published Calculation of the efficiency of worm gear drives Find, read and cite all the research you need on ResearchGate.
1.Calculation of gear ratio (i):
where, NA and NB = speed of the driver and driven respectively, and ZA and ZB = Number of teeth on driver and driven respectively.
2.Selection of material
Consulting Table 5.3, knowing the gear ratio i, choose the suitable material.
3.If not given, assume gear life (say 20000 hrs)
4.Calculation of initial design torque:
[Mt] = Mt . K. Kd
where, [Mt] = transmission torque
K = Load factor, Table 5.11
Kd = Dynamic load factor, Table 5.12
Assume K. Kd = 1.3 ( if not given)
5.Calculation of Eeq, [ϭb] and [ϭc]:
üFrom table 5.20 Calculate Eeq
üFrom table 5.16 Calculate Design bending stress [ϭb]
üCalculate Design contact stress [ϭc] by
[ϭc] = CB . HB. Kcl (or)
[ϭc] = CR . HRC. Kcl
where, CB CR = Coefficient of surface hardness from table 5.18
HB HRC = Hardness number
6. Calculation if centre distance (a):
6.Select number of teeth on gear and pinion:
Worm Gear Design Calculator
ØOn pinion,Z1 = Assume 18
Ø On gear, Z2 = i X Z1
8.Calculation of module:
Choose standard module from table 5.8
9. Revision of centre distance(m)
10. Calculate b, d1, v and ѱp :
Calculate face width, b = ѱ. a
Calculate pitch dia, d = m.z1
Calculate pitch line velocity, v = (πd1N1)/60
Calculate value of ѱp = b/d1
11. Selection of quality of gear:
Knowing the pitch line velocity and consulting table 5.22, select a suitable quality
of gear.
12. Revision of design torque [Mt]: Revise K:
Using the calculated value of ѱp revise the K value by using table 5.11
Revise Kd:
Using the selected quality if gear and pitch line velocity, revise the Kd
value
[Mt] = Mt . K. Kd
13. Check for bending:
14. Check for wear strength:
Calculate induced contact stress,
15. If the design is not satisfactory (ϭb > [ϭb] and / or ϭc > [ϭc] ), then increase the module of face width value of the gear material.
16. Check for gear:
a.Check for bending:
If Ϭb2 ≤ [Ϭb2], then design is safe.
b.Check for wear strength:
Calculate induced contact stress will be same for pinion and gear,
So,
Ϭc2 = Ϭc
üCompare Ϭc and [Ϭc]
üIf Ϭc ≤ [Ϭc], then design is safe
Worm Gear Design Calculation Pdf Viewer Download
Resources:
Spur Gear design formula for geometry, pitch, tooth clearance and critical functional data.
(Inch Units Applicable for Constants)
Where:
φ = Pressure Angle
a = Addendum
aG = Addendum of Gear
aP = Addendum of Pinion
b = Dedendum
c = Clearance
C = Center Distance
D = Pitch Diameter
DG = Pitch Diameter of Gear
DP = Pitch Diameter of Pinion
DB = Base Circle Diameter
DO = Outside Diameter
DR = Root Diameter
F = Face Width
hk = Working Depth of Tooth
ht = Whole Depth of Tooth
mG = Gear Ratio
N = Number of Teeth
NG = Number of Teeth in Gear
NP = Number of Teeth in Pinion
p = Circular Pitch
P=Diametral Pitch
Equations for Standards Spur Gears
| To Find | Equation | |
| Base Circle Pitch | DB = D cosφ | |
| Circular Pitch | p = ( π D )/ N | |
| Center Distance | C = Np (mG + 1) / 2P C = ( Dp + DG ) / 2 C = ( NG + Np ) / 2P C = (NG + Np) p / 2P C = (NG + Np) p / 6.2832 | |
| Diametral Pitch | P = π / p | |
| Gear Ratio | mG = NG / Np | |
| Number of Teeth | N = P D N = ( π D ) / p | |
| Outside Diameter (Full Depth Teeth) | DO = ( N + 2 ) / P DO = [ ( N + 2 ) p ] / π | |
| Outside Diameter (American Standard Stub Teeth) | DO = ( N + 1.6 ) / P DO = [ ( N + 1.6 ) p ] / π | |
| Outside Diameter | DO = D + 2a | |
| Pitch Diameter | D = N / P D = (N p ) / π | |
| Root Diameter | DR = D - 2b | |
| Whole Depth | a + b | |
| Working Depth | aG + ap | |
Gear Calculation Formula Pdf
Formulas for Tooth Parts, 20-and 25-degree Involute Full-depth Teeth
ANSI Coarse Pitch Spur Gear Tooth Forms ANSI B6.1
| To Calculate | Circular Pitch, p, Known |
| Addendum | a = 0.3183 × p |
| Dedendum (Preferred) | b = 0.3979 × p |
| (Shaved or Ground Teeth)a | b = 0.4297 × p |
| Working Depth | hk = 0.6366 × p |
| Whole Depth (Preferred) | ht = 0.7162 × p |
| (Shaved or Ground Teeth) | ht = 0.7480 × p |
| Clearance (Preferred)b | c = 0.0796 × p |
| (Shaved or Ground Teeth) | c = 0.1114 × p |
| Fillet Radius (Rack)c | rf = 0.0955 × p |
| Pitch Diameter | D = 0.3183 × Np |
| Outside Diameter | DO = 0.3183 × (N + 2) p |
| Root Diameter (Preferred) | DR = 0.3183 × (N − 2.5) p |
| Root Diameter (Shaved or Ground Teeth) | DR = 0.3183 × (N − 2.7) p |
| Circular Thickness Basic | t = p / 2 |
Equations Tooth Parts, 20-and 25-degree Involute Full-depth Teeth ANSI Coarse Pitch Spur Gear Tooth Forms ANSI B6.1
a When gears are preshave cut on a gear shaper the dedendum will usually need to be increased to 1.40/P to allow for the higher fillet trochoid produced by the shaper cutter. This is of particular importance on gears of few teeth or if the gear blank configuration requires the use of a small diameter shaper cutter, in which case the dedendum may need to be increased to as much as 1.45/P. This should be avoided on highly loaded gears where the consequently reduced J factor will increase gear tooth stress excessively.
b A minimum clearance of 0.157/P may be used for the basic 20-degree and 25-degree pressure angle rack in the case of shallow root sections and use of existing hobs or cutters.
c The fillet radius of the basic rack should not exceed 0.235/P for a 20-degree pressure angle rack or 0.270/P for a 25-degree pressure angle rack for a clearance of 0.157/P. The basic rack fillet radius must be reduced for teeth with a 25-degree pressure angle having a clearance in excess of 0.250/P.
Helical Gear
When Defined | |
Normal D.P. (Pn) | Pn= P / cos A |
Number of teeth (N) and the Helix Angle (A) | |
Pitch Diameter (D) | Number of teeth (N), the Normal Diametral Pitch and the Helix Angle (A) |
Outside Diameter (OD) | OD = D + (2 X a) |
Normal Diametral Pitch (P) and the Pitch Diameter (D) | |
Helix Angle (A) for Parallel Shaft Drive | Number of Teeth (N), Pitch Diameter (D) and the Diametral Pitch (P) |
Addendum (a) | a = 1 / Pn |
Pitch Diameter (D) and Pitch Helix Angle |
Circular Pitches and Equivalent Diametral Pitches Table
Worm Gear Design Calculation Pdf Viewer Software
Circular Pitch | Module | Addendum | Dedendum or Depth of Space Below Pitch Line | ||||
| 4 | 0.7854 | 32.3402 | 2.0000 | 1.2732 | 2.5464 | 1.4732 | 2.7464 |
| 3 - 1/2 | 0.8976 | 28.2581 | 1.7500 | 1.1140 | 2.2281 | 1.2890 | 2.4031 |
| 3 | 1.0472 | 24.2552 | 1.5000 | 0.9549 | 1.9098 | 1.1049 | 2.0598 |
| 2 - 3/4 | 1.1424 | 22.2339 | 1.3750 | 0.8753 | 1.7506 | 1.0128 | 1.8881 |
| 2 - 1/2 | 1.2566 | 20.2117 | 1.2500 | 0.7957 | 1.5915 | 0.9207 | 1.7165 |
| 2 - 1/4 | 1.3963 | 18.1913 | 1.1250 | 0.7162 | 1.4323 | 0.8287 | 1.5448 |
| 2 | 1.5708 | 16.1701 | 1.0000 | 0.6366 | 1.2732 | 0.7366 | 1.3732 |
| 1 - 7/8 | 1.6755 | 15.1595 | 0.9375 | 0.5968 | 1.1937 | 0.6906 | 1.2874 |
| 1 - 3/4 | 1.7952 | 14.1488 | 0.8750 | 0.5570 | 1.1141 | 0.6445 | 1.2016 |
| 1 - 5/8 | 1.9333 | 13.1382 | 0.8125 | 0.5173 | 1.0345 | 0.5985 | 1.1158 |
| 1 - 1/2 | 2.0944 | 12.1276 | 0.7500 | 0.4775 | 0.9549 | 0.5525 | 1.0299 |
| 1 - 7/16 | 2.1855 | 11.6223 | 0.7187 | 0.4576 | 0.9151 | 0.5294 | 0.9870 |
| 1 - 3/8 | 2.2848 | 11.1169 | 0.6875 | 0.4377 | 0.8754 | 0.5064 | 0.9441 |
| 1 - 5/16 | 2.3936 | 10.6116 | 0.6562 | 0.4178 | 0.8356 | 0.4834 | 0.9012 |
| 1 - 1/4 | 2.5133 | 10.1062 | 0.6250 | 0.3979 | 0.7958 | 0.4604 | 0.8583 |
| 1 - 3/16 | 2.6456 | 9.6010 | 0.5937 | 0.3780 | 0.7560 | 0.4374 | 0.8154 |
| 1 - 1/8 | 2.7925 | 9.0958 | 0.5625 | 0.3581 | 0.7162 | 0.4143 | 0.7724 |
| 1 - 1/16 | 2.9568 | 8.5904 | 0.5312 | 0.3382 | 0.6764 | 0.3913 | 0.7295 |
| 1 | 3.1416 | 8.0851 | 0.5000 | 0.3183 | 0.6366 | 0.3683 | 0.6866 |
| 15/16 | 3.3510 | 7.5798 | 0.4687 | 0.2984 | 0.5968 | 0.3453 | 0.6437 |
| 7/8 | 3.5904 | 7.0744 | 0.4375 | 0.2785 | 0.5570 | 0.3223 | 0.6007 |
| 13/16 | 3.8666 | 6.5692 | 0.4062 | 0.2586 | 0.5173 | 0.2993 | 0.5579 |
| 3/4 | 4.1888 | 6.0639 | 0.3750 | 0.2387 | 0.4775 | 0.2762 | 0.5150 |
| 11/16 | 4.5696 | 5.5586 | 0.3437 | 0.2189 | 0.4377 | 0.2532 | 0.4720 |
| 2/3 | 4.7124 | 5.3903 | 0.3333 | 0.2122 | 0.4244 | 0.2455 | 0.4577 |
| 5/8 | 5.0265 | 5.0532 | 0.3125 | 0.1989 | 0.3979 | 0.2301 | 0.4291 |
| 9/16 | 5.5851 | 4.5479 | 0.2812 | 0.1790 | 0.3581 | 0.2071 | 0.3862 |
| 1/2 | 6.2832 | 4.0426 | 0.2500 | 0.1592 | 0.3183 | 0.1842 | 0.3433 |
| 7/16 | 7.1808 | 3.5373 | 0.2187 | 0.1393 | 0.2785 | 0.1611 | 0.3003 |
| 2/5 | 7.8540 | 3.2340 | 0.2000 | 0.1273 | 0.2546 | 0.1473 | 0.2746 |
| 3/8 | 8.3776 | 3.0319 | 0.1875 | 0.1194 | 0.2387 | 0.1381 | 0.2575 |
| 1/3 | 9.4248 | 2.6947 | 0.1666 | 0.1061 | 0.2122 | 0.1228 | 0.2289 |
| 5/16 | 10.0531 | 2.5266 | 0.1562 | 0.0995 | 0.1989 | 0.1151 | 0.2146 |
| 2/7 | 10.9956 | 2.3100 | 0.1429 | 0.0909 | 0.1819 | 0.1052 | 0.1962 |
| 1/4 | 12.5664 | 2.0213 | 0.1250 | 0.0796 | 0.1591 | 0.0921 | 0.1716 |
| 2/9 | 14.1372 | 1.7967 | 0.1111 | 0.0707 | 0.1415 | 0.0818 | 0.1526 |
| 1/5 | 15.7080 | 1.6170 | 0.1000 | 0.0637 | 0.1273 | 0.0737 | 0.1373 |
| 3/16 | 16.7552 | 1.5160 | 0.0937 | 0.0597 | 0.1194 | 0.0690 | 0.1287 |
| 1/6 | 18.8496 | .5053 | 0.0833 | 0.0531 | 0.1061 | 0.0614 | 0.1144 |
© Copyright 2000 - 2021, by Engineers Edge, LLC www.engineersedge.com
All rights reserved
Disclaimer | Feedback
Advertising | Contact | Privacy Policy
Date/Time: